« Nous sommes une université, pas des bains publics ! »
Qu’il l’ait vraiment prononcée ou non, c’est la seconde phrase que la postérité retient de David Hilbert, le géant des mathématiques de la Belle Époque (la première, on en parlait là). S’il a souligné ainsi l’absurdité de la règle de non-mixité à la faculté de Göttingen, c’est pour pouvoir faire admettre dans le corps professoral sa jeune collègue Emmy Noether.
Emmy Noether est née en 1882 dans le nord de la Bavière: son père Max est mathématicien à l’université d’Erlangen. À 18 ans elle a obtenu un brevet pour enseigner le français et l’anglais dans les établissements de jeunes filles, mais a préféré poursuivre ses études en mathématiques. Ce que l’université accepte à contre-cœur: elle n’est qu’auditrice, et n’a pas le droit de passer les examens. Sur une promotion d’un millier d’étudiants, on compte… 2 jeunes femmes.
Cependant, en 1904 la loi est amendée[1]: Emmy Noether est autorisée à recevoir son diplôme, puis à s’attaquer à une thèse, sous la direction de Paul Gordan. Après l’avoir soutenue fin 1907, elle continue ses recherches en algèbre, en tant qu’assistante de son père… mais bénévolement ! En avril 1915, ses travaux sur les invariants attirent l’attention de Felix Klein et David Hilbert: ils l’invitent à les rejoindre à Göttingen, qui est en train de devenir la capitale mondiale des mathématiques et de la physique[2]. Leur équipe travaille à l’époque sur les équations de la physique, et les aspects mathématiques de la théorie de la relativité générale. À peine est-elle arrivée qu’Emmy Noether, en se penchant sur ces questions, va bâtir le plus beau monument de la physique théorique.
Le plus beau monument de la physique
Un siècle après que Newton avait posé les bases de la mécanique, Joseph-Louis Lagrange avait entrepris de la reformuler sous une forme mathématiquement plus satisfaisante. Plus satisfaisante parce que l’équation de Lagrange garde la même forme, quelques soient les coordonnées dans lesquelles on se place. Et cet aspect « esthétique » est d’importance capitale en physique: si on veut qu’il y ait des lois de la nature, alors ces lois doivent être les mêmes aujourd’hui qu’il y a deux jours ou 2 000 ans, et elles seront les mêmes dans 3 millions d’années. Elles devraient aussi s’écrire de la même façon à Paris et à Göttingen, sur Terre et sur Jupiter. Et enfin il faut qu’elles soient identiques, que l’on soit tourné vers le nord ou le sud, vers le haut ou le bas.
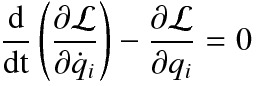
On peut donc se tourner, se déplacer dans le temps ou dans l’espace: à chaque fois que les lois de la physique sont inchangées par une de ces transformations, on parle de symétrie. Or ce genre d’objet mathématique, c’est justement la spécialité d’Emmy Noether. Avec son premier théorème[3], qu’elle publie en 1918, elle démontre que
pour chaque symétrie, il existe une quantité physique qui se conserve au cours du temps.
Si les lois de la physique sont les mêmes à tout instant, alors quelque chose qu’on appelle l’énergie se conserve. Si les lois de la physique sont les mêmes partout, alors la quantité de mouvement se conserve. Et si elles sont les mêmes dans toutes les directions, alors le moment cinétique se conserve. Et vice et versa.
C’est l’un des quelques énoncés capables de provoquer un bref instant d’ébahissement, entre la fascination, le choc esthétique, le déclic de la compréhension, et un soupçon d’incrédulité[4]. Einstein le qualifie immédiatement de « monument de la pensée mathématique ». Et c’est un monument aussi profond et révolutionnaire qu’il est beau, puisqu’il va ensuite service de socle de construction à toute la physique théorique ! C’est désormais en cherchant des symétries qu’on parviendra à identifier de nouvelles quantités invariantes. Et il s’applique partout: en mécanique classique, en relativité, en physique des particules…
Des difficultés d’être la première
Pendant que Noether enchaîne les résultats majeurs, Hilbert fait des pieds et des mains pour lui trouver une place d’enseignante (privatdozentin), mais en vain. Il ne parvient pas à faire fléchir les autres départements de son université, qui s’en tiennent à la loi: le gouvernement prussien a décrété que l’habilitation (à enseigner) était réservée aux hommes. Hilbert demande au ministère de faire une exception (mais pas d’abroger le décret…): il attend deux ans une réponse, et elle est négative. Pendant 4 ans, Emmy Noether va donc donner des cours qui officiellement sont ceux de David Hilbert.
Il lui faut attendre la fin de la première guerre mondiale pour qu’enfin elle soit autorisée à passer son Habilitation. Le 4 juin 1919, Frl. Dr. Noether peut enfin donner son premier cours officiel, devant l’impressionnant aréopage qu’est le département mathématique de Göttingen à l’époque: Hilbert et Klein, mais aussi Courant, Debye, Landau, Voigt, Runge, Prandtl… Toutefois il semble que ses facilités avec l’abstraction n’aient pas fait d’elle une excellente pédagogue pour ses étudiants de premier cycle. En 1922, on lui donne enfin le droit d’encadrer officiellement des thèses… et de percevoir un (petit) salaire[5] ! Son œuvre ultérieure ne touche plus à la physique mais se concentre sur l’algèbre. Avec un succès tel que son nom, comme celui de son mentor, va devenir un adjectif: on parle désormais de groupes, d’anneaux, d’espaces noethériens.
L’exil
En 1932, Emmy Noether fête ses 50 ans, mais n’a toujours pas réussi à obtenir un poste de professeur titulaire. À défaut de faire fléchir l’administration, son œuvre immense lui vaut quand même des hommages de la communauté mathématique: elle obtient une récompense de l’université de Leipzig et elle est la première femme à donner une présentation plénière au Congrès International des Mathématiciens qui se tient cette année-là à Zürich[6].
Le 6 novembre de la même année, le parti nazi remporte les élections législatives. Le 30 janvier 1933, Adolf Hitler devient chancelier. Le 23 mars, il obtient les pleins pouvoirs. Le 7 avril, Emmy Noether, qui est juive, se voit signifier l’interdiction d’enseigner (comme nombre de ses collègues de Göttingen). Fin octobre, elle embarque sur le Bremen, direction la Pennsylvanie, grâce à une invitation de l’université (pour femmes…) de Bryn Mawr. En 1934, elle donne également des cours à Princeton. Le 14 avril 1935, elle décède soudainement à l’hôpital, lors de l’opération d’une tumeur bénigne.
Aller plus loin
- Je me suis basé pour ce billet sur la biographie d’Emmy Noether par Auguste Dick, datant de 1981 et traduite en anglais par Blocher. A ma connaissance il n’y a pas de biographie en français.
- Une petite anecdote: dans le chapitre traitant de sa famille, en constatant le peu d’éléments connus sur la mère de Noether, la biographie ci-dessus rapporte une citation de l’écrivain mathématicien Eric Temple Bell. Celui-ci observe qu’il est typiquement allemand (sic) de s’intéresser uniquement au père, et pas à la mère, dans les biographies. Et il fait cette remarque dans un ouvrage intitulé… « Men of mathematics ».
- Une série qu’on espère longue sur des femmes scientifiques.
- L’eulogie publiée par Einstein dans le New York Times après le décès d’Emmy Noether [en anglais].
- Et pour finir, un livre sur la beauté de la symétrie en physique [en anglais], et un billet de D. Louapre sur un aspect ambivalent de cette quête esthétique.
[1] Pour autant, en 1908 encore le ministre prussien de l’éducation devra rappeler que les professeurs n’ont pas le droit de refuser aux étudiantes l’accès à leurs cours.
[5] . ↑
[6] Il n’y en aura pas d’autre avant 1990. ↑
La Forêt des Sciences 
Pingback: À Göttingen, à Göttingen | La Forêt des Sciences